Mengenal 8 Istilah Dalam Invers Matriks yang Harus Kamu Ketahui

Bagi kamu yang saat ini duduk di bangku Sekolah Menengah Atas (SMA) atau tepatnya kelas 12, pasti sudah tidak asing lagi dengan invers matriks, ‘kan? Atau saat ini justru sedang merasa pusing memikirkan metode matematika yang satu ini?

Invers matriks adalah salah satu metode yang dapat digunakan untuk menyelesaikan sistem persamaan linier tiga variabel.

Cara penyelesaian menggunakan metode ini adalah dengan menggunakan tabel yang terdiri dari variabel tersebut. Dengan begitu, penghitungannya juga menjadi lebih mudah.

Banyaknya variabel yang terdapat di dalam matriks ikut mempengaruhi matriks itu sendiri. Sebuah matriks juga mempunyai sebuah ordo (m x n). metode penyelesaiannya dengan menggunakan invers matriks yang melahirkan beberapa istilah penting.

Berikut ini adalah istilah-istilah yang ada dalam invers matriks. Agar tidak bingung saat mengerjakan soal dengan metode matriks, yuk berkenalan dengan beberapa istilah berikut.

Istilah-istilah Dalam Invers Matriks

istilah-istilah dalam invers matriks

1. Matriks Persegi

Matriks persegi merupakan matriks yang jumlah elemen pada baris dan kolom yang sama. Selain itu, karena bentuknya yang berupa bujur sangkar, maka terdapat diagonal utama serta diagonal sekunder di matriks persegi.

Diagonal utama merupakan bagian diagonal yang menurun ke bawah, contohnya seperti {a11, a22, a33, ………., amn}. Sedangkan diagonal sekunder merupakan bagian dari diagonal yang naik ke atas. Contohnya seperti {am1, a1n, dan sebagainya}.

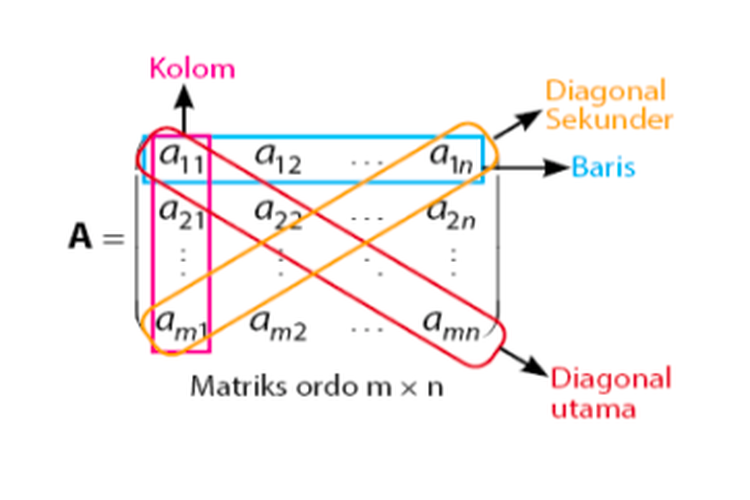Matriks Persegi

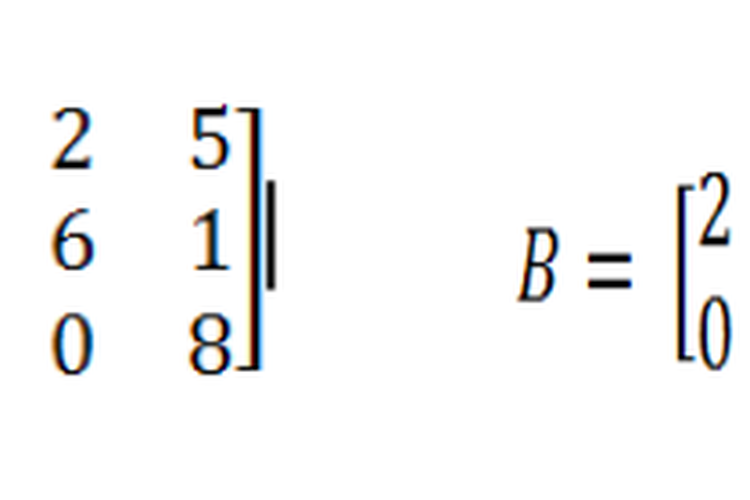Matriks Persegi

2. Matriks Baris

Matriks baris ini merupakan satu matriks yang hanya memiliki satu baris saja, sehingga ordo dari tersebut adalah A1xn. Contoh dari matriks baris ini adalah sebagai berikut:

A= [ 2 0 ] dan B= [ 3 -1 5 0 ].

Matriks A adalah matriks baris berordo 1x2, sedangkan pada matriks B adalah matriks baris yang memiliki ordo 1x4.

3. Matriks Kolom

Matriks kolom merupakan suatu matriks yang hanya memiliki 1 kolom saja. Matriks kolom ini adalah matriks yang memiliki ordo m x 1. Contoh dalam matriks kolom ini adalah sebagai berikut:

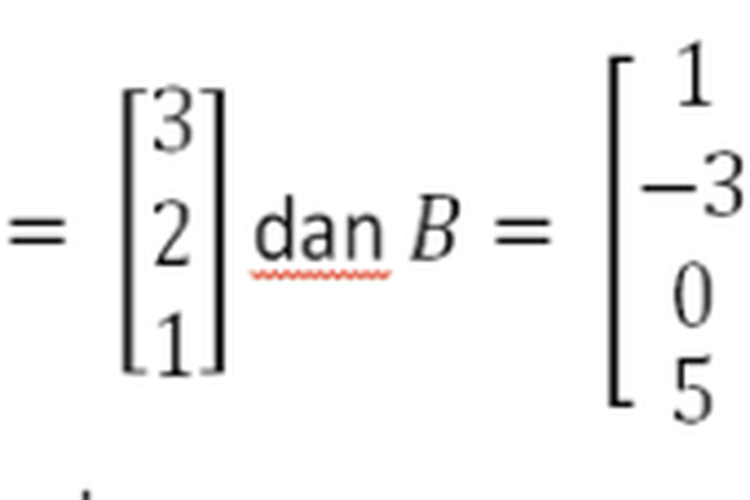Matriks Kolom

Matriks A adalah matriks dari kolom yang memiliki ordo 3 x 1. Sedangkan pada matriks B adalah matriks kolom yang memiliki ordo 4 x 1.

4. Matriks Nol

Matriks nol adalah matriks yang semua elemennya merupakan bilangan nol. Matriks nol dinotasikan sebagai 0mxn. Contoh dari matriks nol adalh seperti berikut ini:

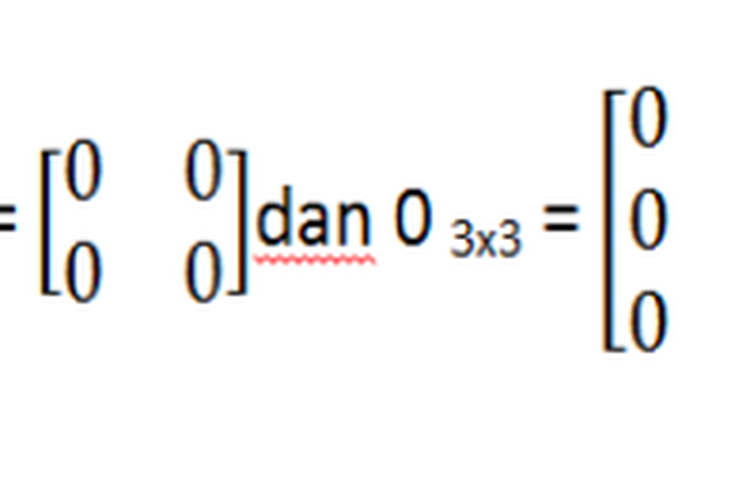Matriks Nol

5. Matriks Identitas

Matriks identitas atau sering disebut dengan matriks satuan merupakan matriks yang semua diagonalnya adalah sama, yaitu memiliki nilai 1. Simbol dari matriks identitas ini adalah | miring ( | ). Contoh dari matriks identitas adalah seperti di bawah ini:

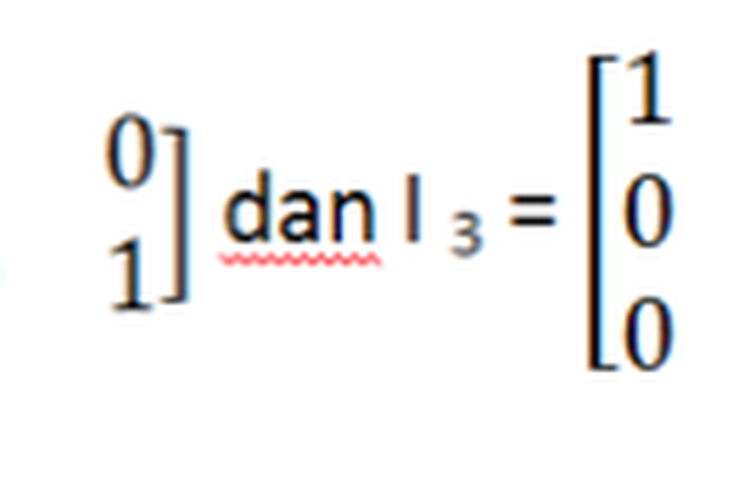Matriks Identitas

6. Matriks Skalar

Matriks skalar merupakan matriks yang elemen-elemen diagonalnya adalah bernilai sama. Jadi, a11=a22=…..=amn=k. Nilai k ini bisa bernilai sembarang. Contoh dari matriks scalar adalah seperti di bawah ini:

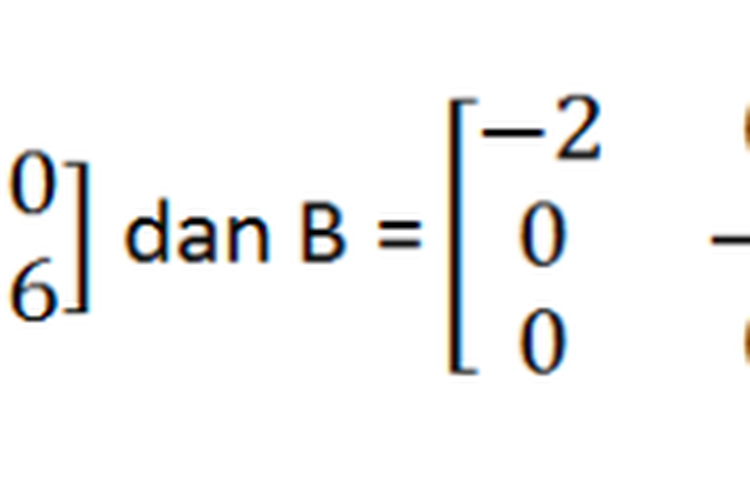Matriks Skalar

Matriks A merupakan matriks skalar yang memiliki ordo 2. Sedangkan pada matriks B adalah matriks scalar yang memiliki ordo 3.

7. Transpose Matriks

Transpose matriks ialah matriks baru yang diperoleh dari dengan menukar letak baris dan kolom dari matriks yang sebelumnya. Transpos matriks disimbolkan dengan memberikan aksen atau T pada bagian atas yang ada di matriks sebelumnya.

8. Invers Matriks

Invers matriks merupakan sebuah kebalikan dari kedua matriks. Di mana jika matriks tersebut dikalikan akan menghasilkan matriks persegi (AB = BA = |). Simbol dari invers matriks adalah pangkat -1 pada bagian atas hurufnya.

Bagaimana, kamu sudah memiliki gambaran tentang invers matriks sekarang? Invers matriks akan menjadi mudah untuk dikerjakan jika kamu mengetahui rumus serta istilah di dalamnya. Selain itu, supaya semakin lihai dalam mengerjakan soal-soal matriks, kamu juga bisa mengasah kemampuan kamu dengan mengerjakan soal-soal latihan.

Kamu bisa mencoba mempelajari buku Logika dan Matematika. Buku ini dapat digunakan sebagai referensi yang dapat menunjang pembelajaran matematika. Dengan buku ini, diharapkan pembaca mampu meningkatkan kemampuannya dalam berpikir logis, kreatif, serta kritis.

Buku ini bisa langsung kamu pesan melalui gramedia.com.

Selain itu, ada gratis voucher diskon yang bisa kamu gunakan tanpa minimal pembelian. Yuk, beli buku di atas dengan lebih hemat! Langsung klik di sini untuk ambil vouchernya.

promo diskon