Cara Mudah Menghitung Luas Permukaan Tabung Beserta Contoh Soal dan Pembahasannya

Dalam Matematika, terdapat sebuah materi pembahasan yang terkait dengan bangun ruang.

Setiap bangun ruang ini tentunya memiliki bentuk yang berbeda-beda sehingga rumus untuk menghitung volumenya juga berbeda.

Tidak semua bangun ruang yang memiliki kesamaan bentuk juga memiliki jumlah volume yang sama karena semua itu didasarkan pada tinggi, luas jari-jari, dan panjang dari bangun ruang itu sendiri.

Bangun ruang tentu berbeda dengan bangun datar, sebab bangun ruang memiliki 3 dimensi sementara bangun datar hanya memiliki 2 dimensi.

Salah satu jenis bangun ruang yang sering ditemukan dalam soal matematika dan memiliki ciri serta volume yang khas adalah tabung.

Berikut adalah penjelasan mengenai tabung dan cara menghitung luas permukaannya yang perlu kamu ketahui.

Pengertian Tabung

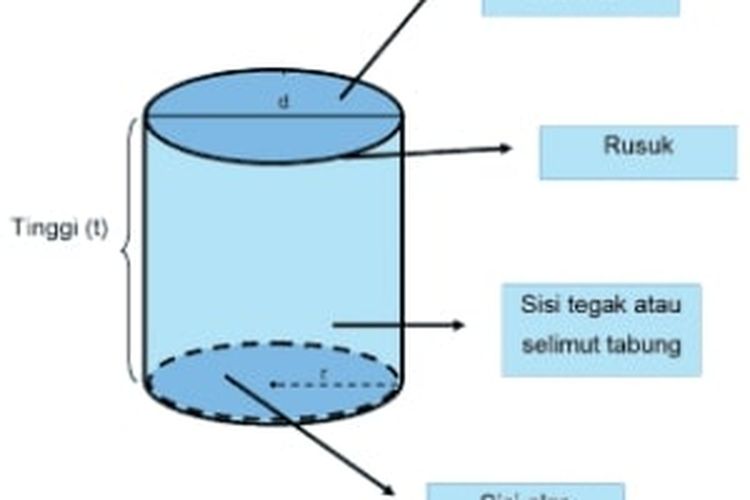
Tabung merupakan jenis bangun ruang 3 dimensi yang pada mulanya terbentuk dari bangun ruang persegi panjang dan 2 buah lingkaran untuk bagian atas dan bawah yang berfungsi sebagai penutup.

Secara umum, tabung memiliki 3 bidang sisi utama yang terdiri dari bidang sisi alas yang disebut alas tabung, bidang lengkung yang disebut selimut tabung, dan bidang atas yang menjadi bagian penutup tabung.

Ciri-Ciri Tabung

Luas Permukaan Tabung

Tabung pada umumnya memang bisa dengan mudah dijumpai dalam kehidupan sehari-hari, terutama yang berkaitan dengan matematika.

Untuk mengetahui bentuk dan ukurannya secara pasti, berikut adalah ciri-ciri tabung yang perlu kamu pahami:

• Memiliki 2 sisi yang berbentuk lingkaran, ada di bagian atas sebagai penutup dan bagian bawah sebagai alas.
• Memiliki 2 bagian rusuk.
• Memiliki 3 sisi yang disebut dengan alas, selimut, dan juga tutup atau penutup.
• Memiliki sisi yang berbentuk persegi panjang.
• Sisi bagian alas dan penutup memiliki ukuran yang sama dan keduanya saling berhadapan.
• Tabung tidak memiliki diagonal bidang dan diagonal ruang.

Cara Menghitung Luas Permukaan Tabung

Perlu kamu pahami kalau luas permukaan merupakan jumlah dari keseluruhan permukaan suatu benda.

Dalam hal ini, luas permukaan tabung sendiri merupakan hasil dari penjumlahan antara luas selimut tabung, luas tutup tabung, dan penjumlahan luas alas pada tabung.

Untuk menghitung keseluruhan luas dari permukaan tabung, rumus yang bisa kamu gunakan adalah sebagai berikut:

Rumus 🡪 L = 2 π r (r + t)

Keterangan:

• L = Luas permukaan tabung.
• π = 3,14 atau 22/7
• r = Jari-jari lingkaran tabung.
• t = Tinggi pada tabung

Cara Menghitung Luas Permukaan Tabung Tanpa Tutup

Tabung tanpa tutup tentunya memiliki perbedaan rumus dan cara penghitungan dengan tabung yang memiliki tutup.

Berikut cara menghitung luas permukaan tabung tanpa tutup:

Rumus 🡪 L = (π x r2) + (2 π r x t)

Keterangan:

• L = Luas permukaan tabung.
• r = Jari-jari lingkaran tabung.
• t = Tinggi pada tabung
• π = 3,14 atau 22/7

Agar kamu lebih mudah memahami rumus penghitungan tabung, berikut adalah beberapa contoh soal beserta pembahasannya yang bisa kamu jadikan bahan pembelajaran di rumah.

Contoh Soal dan Pembahasannya

1. Contoh Soal

Bayu ingin membuat kursi belajar dari batang pohon berbentuk tabung dengan tinggi 50 cm dan panjang diameternya 28 cm.

Jadi, berapa luas permukaan batang pohon tersebut?

Diketahui:

r = ½ diameter 🡪 14 cm

t = 50 cm

d = 28 cm

Cara Menghitung:

Rumus 🡪 2 π r (r + t)

2 x 22/7 x 14 (14 + 50)

88 cm x 64 cm

5.632 cm2

Jadi dapat disimpulkan bahwa luas permukaan batang pohon tersebut adalah 5.632 cm2.

2. Contoh Soal

Sebuah tabung memiliki jari-jari 10 cm.

Jika tinggi tabung tersebut 30 cm dan π = 3,14, berapa luas permukaannya?

Diketahui:

r = 10 cm

t = 30 cm

π = 3,14

Cara Menghitung:

Rumus 🡪 2 π r (r + t)

2 x 3,14 x 30 (10 + 30)

2.512

Jadi dapat disimpulkan bahwa luas permukaan batang pohon tersebut adalah 2.512.

Itu dia beberapa contoh soal dan pembahasannya yang berkaitan dengan luas permukaan tabung.

Bagaimana, mudah bukan?

Tidak hanya materi bangun ruang, matematika juga termasuk salah satu mata pelajaran yang terkenal memiliki banyak sekali materi pembahasan.

Kalau kamu mau mengetahui beberapa trik jago matematika tapi tidak mau mengeluarkan banyak biaya, kamu bisa menemukannya dalam buku Master Trick Ala Bimbel Matematika SMA yang ditulis oleh Tim Tentor Master.

Buku ini berisi kumpulan soal-soal dari Ujian Nasional, SBMPTN, dan Ujian Mandiri yang bisa kamu kerjakan agar kamu semakin terbiasa menghadapi soal matematika dengan berbagai macam tingkat kesulitan.

Tidak hanya itu, buku ini juga menyediakan berbagai macam tips dan trik untuk bisa mengerjakan soal-soal matematika dengan mudah dan cepat, tanpa kamu harus mengikuti bimbel.

Jika tertarik, kamu bisa segera memiliki buku ini dengan membelinya melalui Gramedia.com.