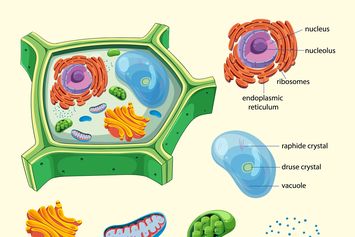
Bagaimana Cara Mencari Invers Matriks? Temukan Jawabannya di Sini!
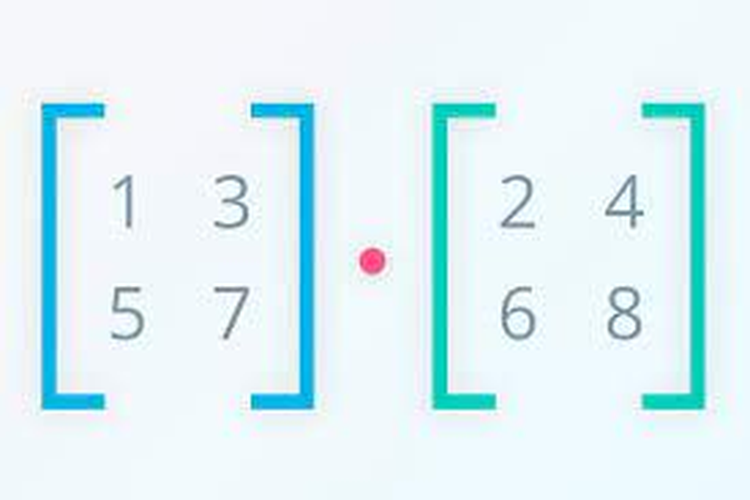 cara mencari invers matriks
cara mencari invers matriks Salah satu topik pembahasan yang penting dalam matriks adalah membahas tentang invers matriks atau kebalikan dari matriks. Invers adalah kebalikan atau lawan dari sesuatu. Sehingga, invers matriks adalah matriks bar yang merupakan kebalikannya dari matriks asal.
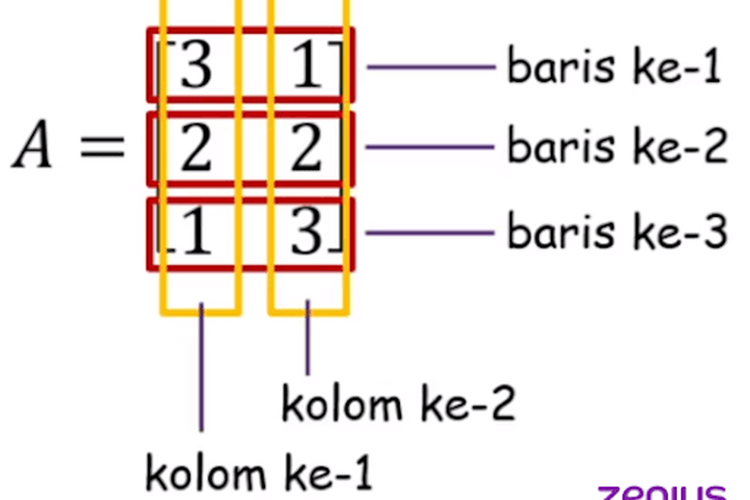
Matriks adalah susunan dengan bentuk persegi panjang atau persegi yang tersusun dari angka-angka dan diatur ke dalam sebuah baris ataupun kolom. Perlu diingat juga, baris merupakan susunan horizontal, sedangkan kolom adalah susunan vertikal.
 cara mencari invers matriks
cara mencari invers matriksSetelah mengetahui definisi dari invers matriks, kemudian pertanyaan selanjutnya adalah bagaimana cara mencari invers matriks? Berikut ulasannya.
Konsep Invers Matriks
Invers matriks A adalah suatu matriks baris yang merupakan kebalikan dengan matriks A dengan notasi A-1. Apabila matriks tersebut dikalikan dengan invers matriksnya, maka akan membentuk matriks identitas.
Ketika kita mengalikan suatu angka dengan kebalikannya, maka nilainya akan menjadi 1.
Biasanya, penggunaan matriks ini hanya untuk memecahkan sistem persamaan linier (SPL). Untuk menyelesaikan invers matriks ini, ada beberapa aturan yang berdasarkan pada ordo matriks, yaitu 2x2 dan 3x3. Dari kedua matriks persegi ini kalian dapat mencari determinannya untuk bisa mencari invers matriks.
Bagaimana Cara Mencari Invers Matriks?
1. Invers Matriks Berordo 2x2
Diketahui matriks di bawah ini
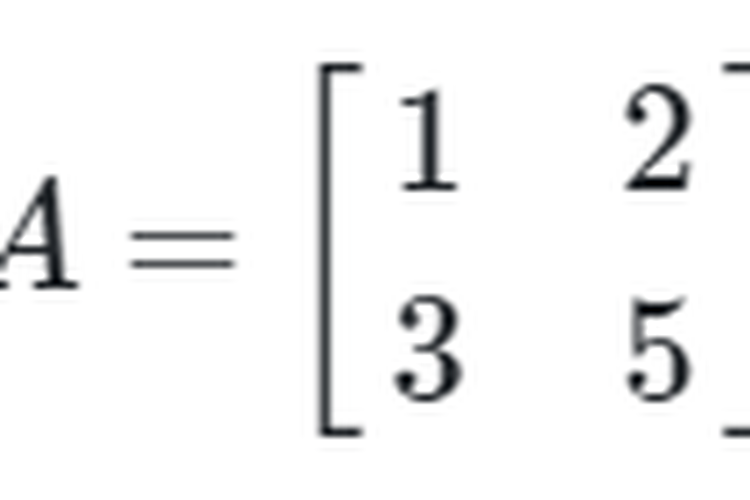 Invers Matriks Berordo 2x2
Invers Matriks Berordo 2x2
Dengan determinan A adalah
|a|= (1x5) – (2x3) = 5-6 = -1
Misalkan lagi matriks C adalah matriks yang diperoleh dengan menukarkan tempat elemen diagonal utama dan juga mengganti tanda dari elemen diagonal kedua matriks A, yaitu
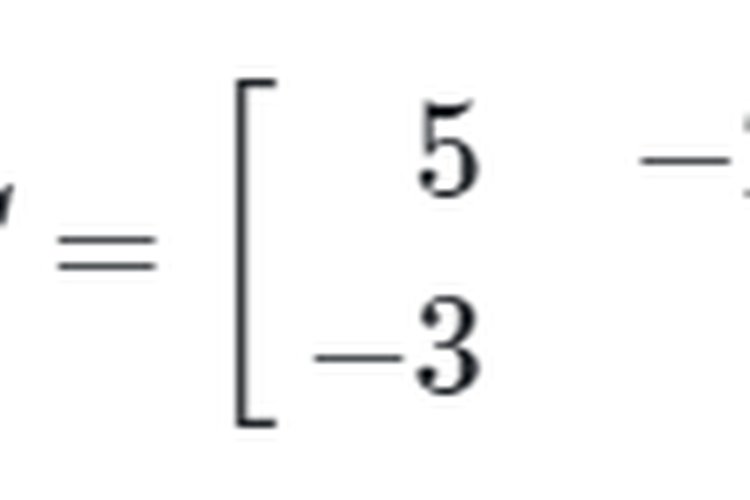 Invers Matriks Berordo 2x2
Invers Matriks Berordo 2x2
Kemudian, bila terdapat matriks B yang didefinisikan sebagai
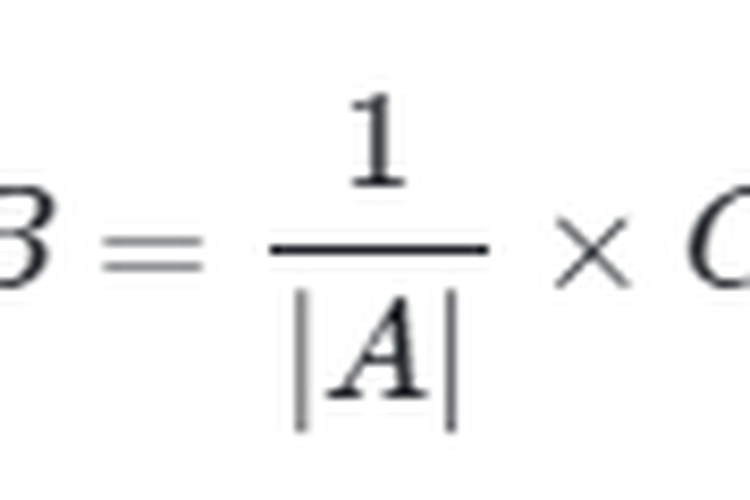 Invers Matriks Berordo 2x2
Invers Matriks Berordo 2x2
Maka,
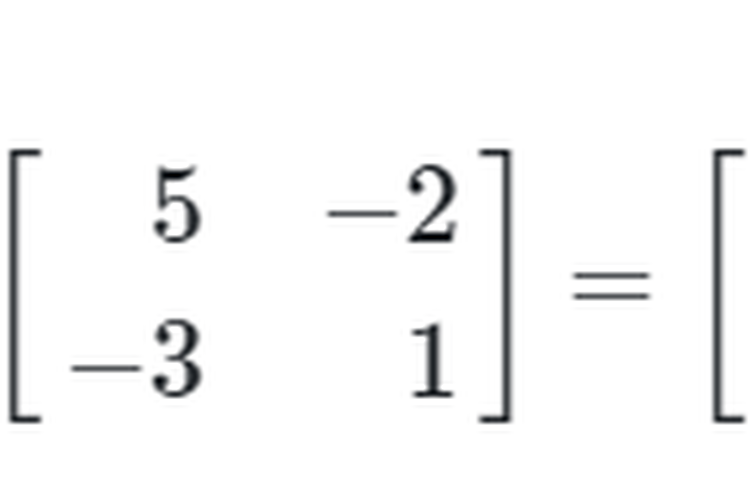 Invers Matriks Berordo 2x2
Invers Matriks Berordo 2x2
Selanjutnya, kamu bisa perhatikan perkalian antara dua matriks A dan B berikut ini:
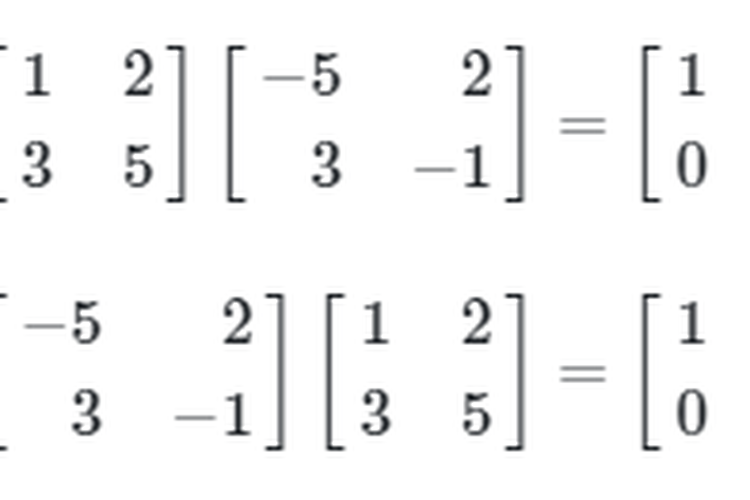 Invers Matriks Berordo 2x2
Invers Matriks Berordo 2x2
Baca buku sepuasnya di Gramedia Digital Premium
Bisa dilihat jika hasil kali dari kedua matriks A dan B adalah AB = BA = |, adalah matriks identitas. Dua matriks seperti itu dikatakan berkebalikan atau saling invers. Matriks A disebut dengan invers matriks B dan matriks B disebut dengan invers matriks A.
Dikatakan juga bahwa matriks A mempunyai invers, yaitu matriks B. Dengan begitu, matriks A akan memiliki invers, kalau ada matriks B sedemikian, sehingga AB = BA = |.
Berikut ini adalah syarat jika suatu matriks A mempunyai invers.
- Jika |A| = 0, maka matriks A tidak mempunyai invers. Matriks A disebut dengan matriks singular.
- Jika |A| ≠ 0, maka matriks A mempunyai invers. Matriks A yang demikian disebut dengan matriks non-singular.
Dari uraian yang disebut di atas, maka bisa disimpulkan bahwa matriks A yang memiliki ordo 2x2 yaitu
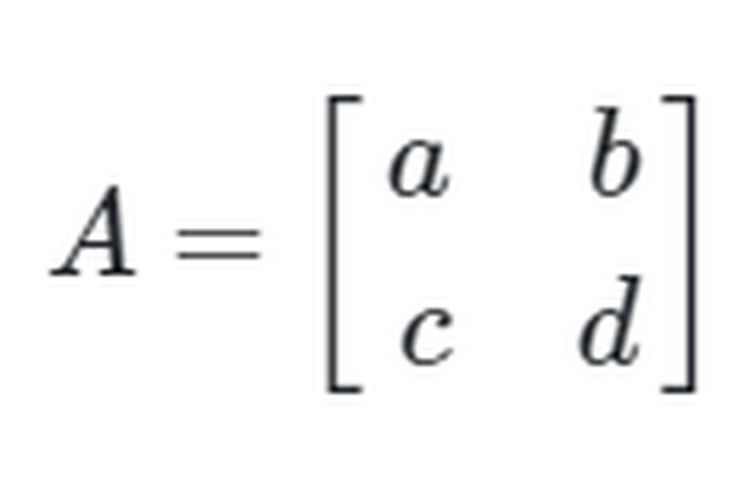 Invers Matriks Berordo 2x2
Invers Matriks Berordo 2x2
Maka bisa ditentukan inversnya yaitu
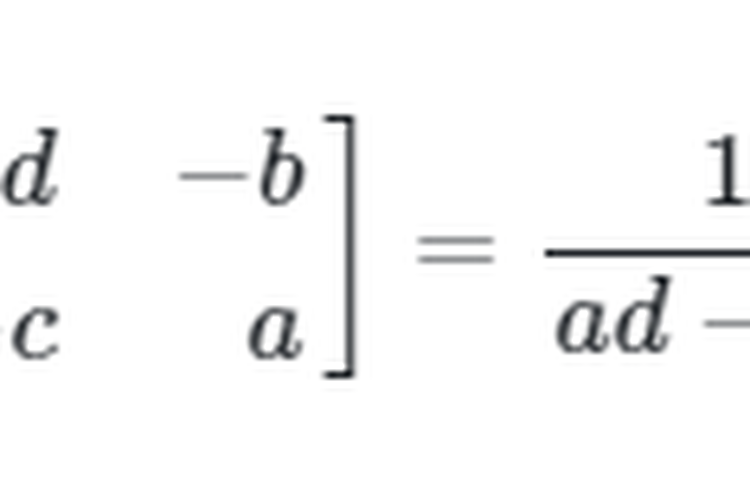 Invers Matriks Berordo 2x2
Invers Matriks Berordo 2x2
2. Invers Matriks Berordo 3x3
Untuk menemukan invers matriks yang memiliki ordo 3x3, kita perlu lebih dulu mengenal apa yang disebut dengan minor entri, kofaktor, dan adjoint. Misalnya terdapat matriks
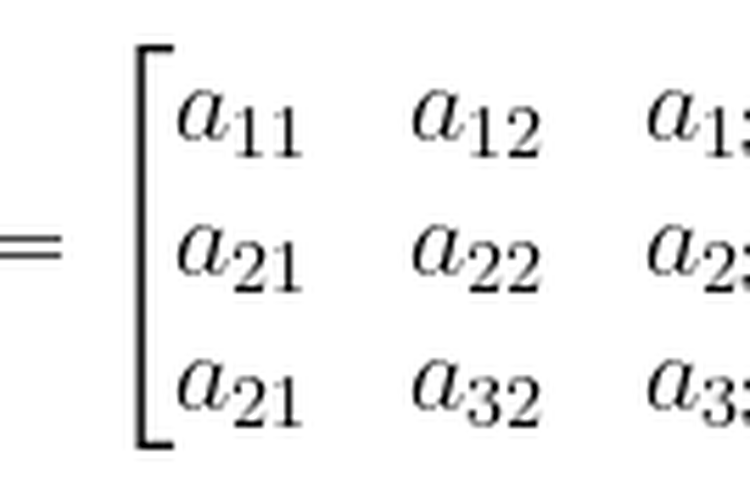 Invers Matriks Berordo 3x3
Invers Matriks Berordo 3x3Minor entri aij yang dinotasikan dengan Mij didefinisikan sebagai suatu determinan submatriks setelah baris ke-i dan kolom ke-j dicoret dari A. maka, bilangan (-1)(i+j)Mij yang dinotasikan Cij disebut dengan kofaktor entri aij.
Perhatikan bahwa kofaktor dan juga minor elemen aij hanya memiliki perbedaan dalam tandanya, yakni, Cij = ±Mij. Cara cepat untuk menentukan apakah penggunaan tanda + atau tanda – didasarkan pada kenyataan bahwa tanda yang menghubungkan Cij dan Mij berada pada garis ke i dan kolom ke j dari susunan, seperti berikut ini
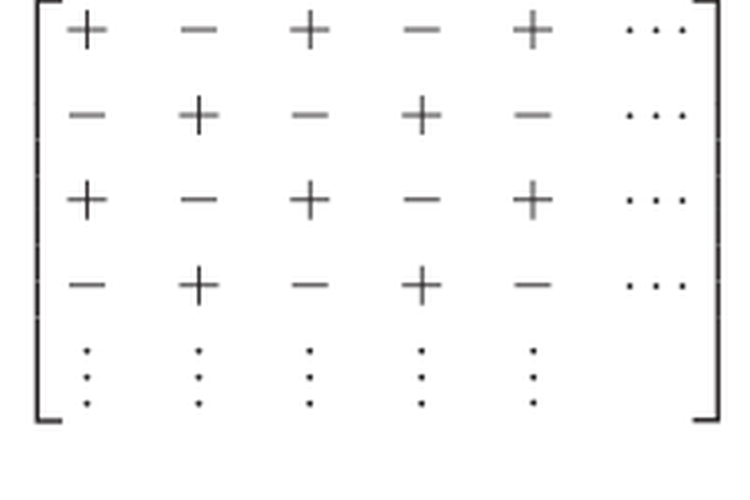 Invers Matriks Berordo 3x3
Invers Matriks Berordo 3x3Untuk kamu yang ingin mempelajari serta memahami lebih lanjut tentang invers matriks dan matematika lainnya, kamu bisa mempelajari melalui buku-buku yang berkaitan. Salah satunya adalah buku Terapan Grup Matriks Atas Ring Komutatif Pada Protokol Perjanjian Kunci.
Buku ini membahas mengenai pembentukan grup matriks atas ring komutatif berhingga yang merupakan bagian perumuman dari grup matriks atas lapangan berhingga. Keduanya membutuhkan dasar konsep teori bilangan, grup berhingga, ring kumulatif berhingga, ring lokal, serta ruang vektor beserta dengan sifatnya.
Buku ini membantu kamu dalam memberikan wacana terapan aljabar abstrak, khususnya pada grup matriks atas ring komutatif berhingga pada kriptografi yang digunakan untuk pengamanan sebuah data.
Buku ini bisa langsung kamu pesan melalui gramedia.com.
Selain itu, ada gratis voucher diskon yang bisa kamu gunakan tanpa minimal pembelian. Yuk, beli buku di atas dengan lebih hemat! Langsung klik di sini untuk ambil vouchernya.
 promo diskon
promo diskon
Terkini Lainnya